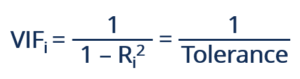El análisis de regresión es una herramienta esencial en la estadística para comprender las relaciones entre variables. Sin embargo, al realizar un análisis de regresión múltiple, es fundamental considerar los efectos de la multicolinealidad. Aquí es donde entra en juego el Factor de Inflación de Varianza (VIF), una medida que nos indica cuánto influye cada variable independiente en la varianza de otras variables en el modelo de regresión. En este artículo, exploraremos en detalle qué es el VIF, cómo se calcula y cómo interpretar sus resultados. Descubre cómo utilizar esta herramienta para mejorar la interpretación y robustez de tus análisis de regresión múltiple.
Una medida de la gravedad de la multicolinealidad en el análisis de regresión.
Más de 1,8 millones de profesionales utilizan CFI para aprender contabilidad, análisis financiero, modelado y más. Comience con una cuenta gratuita para explorar más de 20 cursos siempre gratuitos y cientos de plantillas financieras y hojas de trucos.
¿Qué es el factor de inflación de varianza (VIF)?
El factor de inflación de varianza (VIF) mide la gravedad de la multicolinealidad en el análisis de regresión. Es un concepto estadístico que indica el aumento de la varianza de un coeficiente de regresión debido a la colinealidad.
Resumen
- El factor de inflación de la varianza (VIF) se utiliza para detectar la gravedad de la multicolinealidad en el análisis de regresión de mínimos cuadrados ordinarios (OLS).
- La multicolinealidad aumenta la varianza y el error tipo II. Esto hace que el coeficiente de una variable sea consistente pero poco confiable.
- VIF mide el número de varianzas infladas causadas por la multicolinealidad.
Factor de inflación de varianza y multicolinealidad.
En el análisis de regresión de mínimos cuadrados ordinarios (OLS), la multicolinealidad ocurre cuando dos o más de las variables independientes tienen una relación lineal entre ellas. Por ejemplo, para analizar la relación entre el tamaño de la empresa y las ventas y los precios de las acciones en un modelo de regresión, la capitalización de mercado y las ventas son las variables independientes.
La capitalización de mercado de una empresa y sus ingresos totales están altamente correlacionados. Cuando una empresa genera crecientes ventas, también crece en tamaño. Esto conduce a un problema de multicolinealidad en el análisis de regresión MCO. Cuando las variables independientes en un modelo de regresión tienen una relación lineal perfectamente predecible, se denomina multicolinealidad perfecta.
Con multicolinealidad, los coeficientes de regresión siguen siendo consistentes pero ya no son confiables porque los errores estándar están inflados. Esto significa que el poder predictivo del modelo no se reduce, pero los coeficientes pueden no ser estadísticamente significativos con el error Tipo II.
Entonces, si los coeficientes de las variables no son individualmente significativos, no pueden rechazarse en la prueba t o, pero juntos pueden explicar la varianza de la variable dependiente con rechazo en la prueba t. prueba F y un alto coeficiente de determinación (R2), podría haber multicolinealidad. Es uno de los métodos para detectar multicolinealidad.
VIF es otra herramienta comúnmente utilizada para detectar si existe multicolinealidad en un modelo de regresión. Mide cuánto aumenta la varianza (o error estándar) del coeficiente de regresión estimado debido a la colinealidad.
Usando el factor de inflación de varianza
El VIF se puede calcular utilizando la siguiente fórmula:
Dónde RI2 representa el coeficiente de determinación no ajustado para la regresión de iTh variable independiente sobre el resto. El recíproco de VIF se conoce como tolerancia. Dependiendo de las preferencias personales, se puede utilizar VIF o Tolerancia para detectar multicolinealidad.
Si RI2 es igual a 0, la varianza de las variables independientes restantes no se puede predecir a partir de iTh variable independiente. Por lo tanto, si VIF o Tolerancia es igual a 1, es decir iTh La variable independiente no está correlacionada con el resto de variables, lo que significa que no hay multicolinealidad en este modelo de regresión. En este caso la varianza de iTh El coeficiente de regresión no es excesivo.
En general, un VIF superior a 4 o una tolerancia inferior a 0,25 indica que puede haber multicolinealidad y es necesaria una mayor investigación. Si el VIF es superior a 10 o la tolerancia es inferior a 0,1, existe una multicolinealidad significativa que debe corregirse.
Sin embargo, también hay situaciones en las que los VFI elevados pueden ignorarse de forma segura sin provocar multicolinealidad. A continuación se presentan tres de estas situaciones:
1. Los VIF altos sólo existen en las variables de control, pero no en las variables de interés. En este caso, las variables de interés no son colineales entre sí ni con las variables de control. Los coeficientes de regresión no se ven afectados.
2. Cuando los VIF elevados se deben a la inclusión de productos o potencias de otras variables, la multicolinealidad no tiene ningún impacto negativo. Por ejemplo, un modelo de regresión incluye tanto x como x2 como sus variables independientes.
3. Si una variable ficticia que representa más de dos categorías tiene un VIF alto, la multicolinealidad no está necesariamente presente. Las variables siempre tienen VIF altos cuando solo hay una pequeña proporción de casos en la categoría, independientemente de si las variables categóricas están correlacionadas con otras variables.
Corrección de multicolinealidad
Debido a que la multicolinealidad aumenta la varianza de los coeficientes y causa errores de tipo II, es importante detectarla y corregirla. Existen dos métodos simples y comúnmente utilizados para corregir la multicolinealidad, como se enumeran a continuación:
1. La primera es eliminar una (o más) de las variables altamente correlacionadas. Dado que la información proporcionada por las variables es redundante, el coeficiente de determinación no se ve afectado significativamente por la distancia.
2. El segundo método consiste en utilizar el análisis de componentes principales (PCA) o la regresión de mínimos cuadrados parciales (PLS) en lugar de la regresión MCO. La regresión PLS puede reducir las variables a un conjunto más pequeño sin ninguna correlación entre ellas. En PCA, se crean nuevas variables no correlacionadas. Minimiza la pérdida de información y mejora la previsibilidad de un modelo.
Más recursos
CFI es el proveedor oficial del programa de certificación global Business Intelligence & Data Analyst (BIDA)®, diseñado para ayudar a cualquier persona a convertirse en un analista de clase mundial. Para avanzar aún más en su carrera, los siguientes recursos adicionales le serán útiles: