En el mundo del análisis de datos y la estadística, existen diversas herramientas y métodos para medir y comparar resultados. La puntuación Z y la puntuación T son dos de estos métodos ampliamente utilizados en diferentes campos. Pero, ¿en qué se diferencian y cómo se aplican? En este artículo, exploraremos las diferencias entre la puntuación Z y la puntuación T, y cómo pueden ayudarnos a tomar decisiones basadas en datos confiables y precisos. ¡Descubre cuál de estos dos métodos es más relevante para tu investigación y análisis estadístico!
Diferencia entre puntuación Z y puntuación T
La puntuación Z es una conversión de datos sin procesar a una puntuación estándar cuando la conversión se basa en la media poblacional y la desviación estándar de la población. Podemos calcular la puntuación Z si hay disponible un conjunto de datos completo. La puntuación Z resta la media poblacional de la puntuación bruta y divide el resultado por la desviación estándar de la población. La puntuación t convierte datos sin procesar en la puntuación estándar cuando la conversión se basa en la media y la desviación estándar de la muestra. Si el conjunto de datos de la población no está disponible, debemos recopilar algunos datos de muestra para calcular la media muestral y la desviación estándar de la población.
puntuación Z
Una distribución normal, cuando se dispone de datos completos, está a una distancia de la media. Su fórmula es la siguiente:
Z= (x-μ)/σ
Dónde,
- X = datos brutos individuales
- μ = media poblacional
- σ = desviación estándar de la población
puntuación t
La puntuación t consiste en restar la desviación estándar individual de la media individual y luego dividir el resultado por la desviación estándar general de la muestra multiplicada por el tamaño de la muestra. Su fórmula es la siguiente:
t = {(- μ)/s}*
- = media muestral
- μ = media poblacional
- s = desviación estándar de la muestra
- n = tamaño de la muestra
Pongamos un ejemplo para entender mejor lo mismo:
Hay tres divisiones en una obra: I, II y III. Supongamos que el número de estudiantes que respondieron “I” correctamente es el 25%, es decir, el 75% no puede responder correctamente la pregunta. Asimismo, sea del 10% y 20%, respectivamente, por el número de personas que respondieron correctamente las fracciones II y III; Esto significa que el 90% y el 80% respectivamente encontraron las secciones II y III. Suponemos que la capacidad medida por estos tres ítems es igual y está normalmente distribuida.
La puntuación de cada estudiante en una clase se utiliza para calcular la media de las calificaciones sobre 50 y una desviación estándar de 10. Podemos calcular el puntaje Z con puntaje 50 como (50-50) / 10 = 0
Podemos interpretar que la puntuación del alumno está a una distancia de 0 (en unidades de desviación estándar) de la media, por lo que el alumno ha conseguido una puntuación media.
Si el valor es 60, la puntuación Z es (60-50)/10 = 1
Podemos interpretar que el estudiante obtuvo una puntuación superior al promedio: una distancia de 1 desviación estándar por encima de la media.
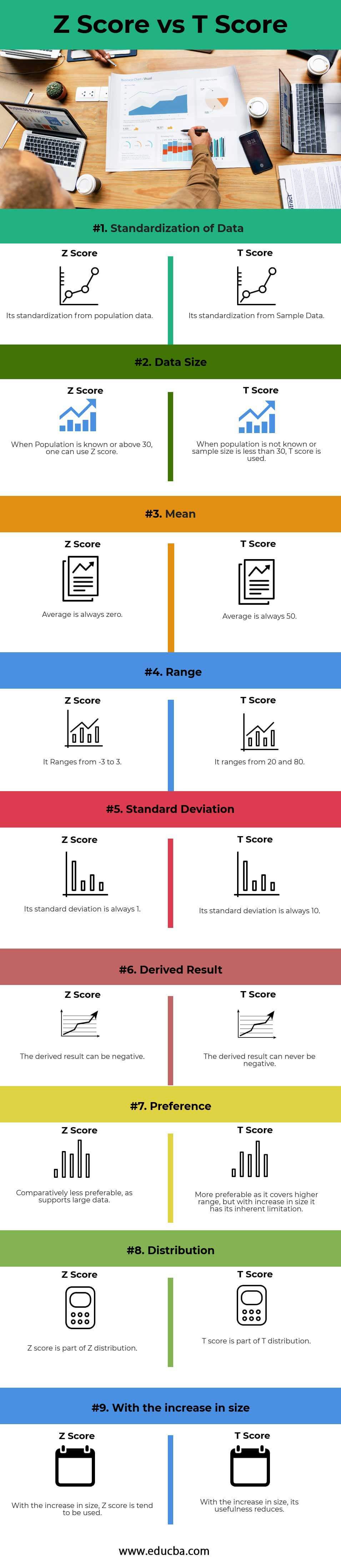
Comparación directa entre Z-Score y T-Score (Infografía)
A continuación se muestran las 9 diferencias clave entre el puntaje Z y el puntaje T:
Diferencias clave entre el puntaje Z y el puntaje T
Analicemos algunas de las diferencias clave entre el puntaje Z y el puntaje T.
- La puntuación Z es la estandarización de los datos de la población sin procesar o más de 30 datos de muestra a una puntuación estándar, mientras que la puntuación T es la estandarización de los datos de muestra de menos de 30 datos a una puntuación estándar.
- La puntuación Z oscila entre -3 y 3, mientras que la puntuación T oscila entre 20 y 80.
- A medida que aumenta el tamaño de los datos, la distribución tiende a ser Z. La distribución del puntaje Z versus el puntaje T es parte de una distribución normal, pero difiere según el tamaño.
- El puntaje Z se utiliza en los datos del mercado de valores para examinar la probabilidad de que una empresa quiebre. Por el contrario, la puntuación t se utiliza a menudo para comprobar la densidad mineral ósea y evaluar el riesgo de fractura.
Tabla comparativa Z-Score vs. T-Score.
Veamos las 9 mejores comparaciones entre las puntuaciones Z y T.
| No Señor. | Puntos de comparación | puntuación Z | puntuación t |
| 1 | Estandarización de datos | Su estandarización basada en datos de población. | Su estandarización a partir de datos de muestra. |
| 2 | Tamaño de datos | Si la población es conocida o tiene más de 30 años, se puede utilizar el puntaje Z | La puntuación T se utiliza cuando se desconoce la población o el tamaño de la muestra es inferior a 30. |
| 3 | Significar | Un promedio siempre es cero. | El promedio es siempre 50. |
| 4 | Rango | El valor está entre -3 y 3. | Está entre 20 y 80. |
| 5 | Desviación Estándar | Su desviación estándar es siempre 1 | Su desviación estándar es siempre 10 |
| 6 | Resultado derivado | El resultado obtenido puede ser negativo. | El resultado obtenido nunca puede ser negativo. |
| 7 | preferencia | Comparativamente menos preferible ya que admite grandes conjuntos de datos | Más preferido porque cubre un área más grande, pero a medida que aumenta el tamaño tiene sus limitaciones inherentes. |
| octavo | distribución | La puntuación Z es parte de la distribución Z. | La puntuación t es parte de la distribución T |
| 9 | con la ampliación | A medida que aumenta el tamaño, se tiende a utilizar el puntaje Z. | A medida que aumenta el tamaño, disminuye su utilidad. |
Diploma
Tanto el puntaje Z como el puntaje T son parte de la prueba de hipótesis bajo una distribución normal. Si tiene un conjunto de medidas para diferentes métricas, puede usar puntuaciones z para determinar cómo se clasifican los resultados en sus distribuciones. Entonces puedes compararlos. La estandarización de resultados es una práctica común en la investigación y la planificación porque facilita la comparación de diferentes resultados de pruebas. Estandarizar los resultados antes de combinarlos ayuda al investigador a lograr resultados mejores y comparables.
Artículos recomendados
Esto fue una indicación de la mayor diferencia entre el puntaje Z y el puntaje T. Aquí también analizamos las diferencias clave entre las puntuaciones Z y T mediante infografías y una tabla comparativa. También puedes echar un vistazo a los siguientes artículos para obtener más información:
- Finanzas versus economía
- Comprar activos versus comprar acciones
- Mercado monetario versus mercado de capitales
- Descripción general de la puntuación Z de Altman