¿Alguna vez te has preguntado cuánto vale una cantidad de dinero en el futuro, en términos de valor actual? ¡No te preocupes más! En este artículo, te explicaremos qué es la fórmula del valor actual (PV) y cómo puedes utilizar una calculadora para descubrirlo. No te pierdas esta herramienta invaluable para la toma de decisiones financieras inteligentes. ¡Sigue leyendo para aprender más!
La fórmula del valor actual (PV) es una herramienta fundamental en el mundo financiero para determinar el valor actual de una inversión o flujo de efectivo. Su aplicación es clave para evaluar proyectos, decisiones de inversión y cualquier tipo de transacción económica. En este artículo, te mostraremos cómo calcular el valor actual utilizando esta fórmula y, para facilitarte el proceso, también te presentaremos una calculadora online que hará todos los cálculos por ti. ¡Descubre cómo el PV puede ser tu aliado en el mundo de las finanzas y cómo hacer su cálculo de manera sencilla y precisa! No pierdas la oportunidad de maximizar tus decisiones financieras, ¡sigue leyendo!
¿Qué es una pensión?
A pensión Es un tipo de bono que proporciona al tenedor un flujo de pagos de intereses regulares hasta el vencimiento.

¿Cómo funciona una pensión?
Una anualidad proporciona pagos regulares durante un número específico de años hasta el vencimiento.
Las pensiones son una forma especial de seguridad financiera debido a las siguientes características:
- Pagos regulares → Las anualidades son una fuente común de ingresos para la jubilación porque los valores proporcionan al emisor un flujo constante de pagos a intervalos regulares.
- Sin reembolso de capital a tanto alzado→ Lo que es único acerca de las anualidades es que no hay un pago global final (es decir, el monto principal) que se devuelve al final del plazo del préstamo, similar a los bonos de cupón cero.
- Fecha de vencimiento predefinida → A diferencia de una anualidad perpetua, una anualidad también viene con una fecha de vencimiento predeterminada, que marca el día en que se recibe el último pago de intereses.
- Mismos pagos a plazos. → Dado que no existe un reembolso final del capital, todos los pagos son del mismo valor. Sin embargo, los pagos recibidos antes son más valiosos debido al «valor del dinero en el tiempo«.
Los flujos de efectivo anteriores se pueden reinvertir antes y durante un período de tiempo más largo, de modo que estos flujos de efectivo tengan el valor más alto (y viceversa para los flujos de efectivo recibidos más tarde).
Normalmente, los tipos más comunes de emisores de bonos son los siguientes:
- Compañías de seguros (por ejemplo, planes de pensiones)
- Fondos de inversión
- Casas de bolsa
- Hipoteca y financiación de automóviles
Valor actual de la fórmula de pensión (PV)
El valor presente (PV) de una anualidad es el valor descontado de los pagos futuros del bono, ajustado por una tasa de descuento apropiada requerida por el concepto de Valor del Dinero en el Tiempo (TVM).
La fórmula para calcular el valor presente (PV) de una anualidad es la suma de todos los pagos futuros de la anualidad dividida por uno más el rendimiento al vencimiento (YTM) y elevado a la potencia del número de períodos.
Valor presente de la anualidad (PV) = Σ A ÷ (1 + r) ^ t
Dónde:
- PV = valor presente
- A = pago de pensión por período ($)
- t = número de períodos
- r = Rendimiento al vencimiento (YTM)
Alternativamente, un enfoque más simple consta de los dos pasos siguientes:
- Primero, el pago de la anualidad se divide por el rendimiento al vencimiento (YTM), que se denomina «r» en la fórmula.
- A continuación, el resultado del paso anterior se multiplica por menos. [one divided by (one + r) raised to the power of the number of periods].
Valor presente (PV) de la anualidad = (A ÷ r) (1 – (1 ÷ (1 + r) ^ T))
¿Cuál es la diferencia entre una anualidad ordinaria y una anualidad vencida?
Al calcular el valor presente (PV) de una anualidad, el momento del pago es un factor a considerar.
- Pensión ordinaria → Flujos de efectivo recibidos al final del período
- Pensión adeudada → Flujos de efectivo recibidos al inicio del período.
El término “anualidad adeudada” significa recibo de pago al comienzo de cada período (por ejemplo, alquiler mensual).
Por otra parte, una “anualidad normal” es más adecuada para la planificación de la jubilación a largo plazo porque se realiza un pago fijo (o variable) al final de cada mes (por ejemplo, un contrato de anualidad con una compañía de seguros).
- Pensión fija: La compañía de seguros proporciona intereses en forma de pagos periódicos que deben alcanzar el umbral mínimo de rentabilidad.
- Pensión variable: La compañía de seguros permite a los propietarios invertir sus pagos de pensiones en ciertos vehículos de inversión de bajo riesgo, como fondos mutuos.
La desventaja de las anualidades fijas es que un propietario podría perderse cambios en las condiciones del mercado que habrían sido favorables en términos de rendimiento, pero las anualidades fijas ofrecen una mayor previsibilidad.
Valor actual de una tabla de pensiones ordinaria (PV)
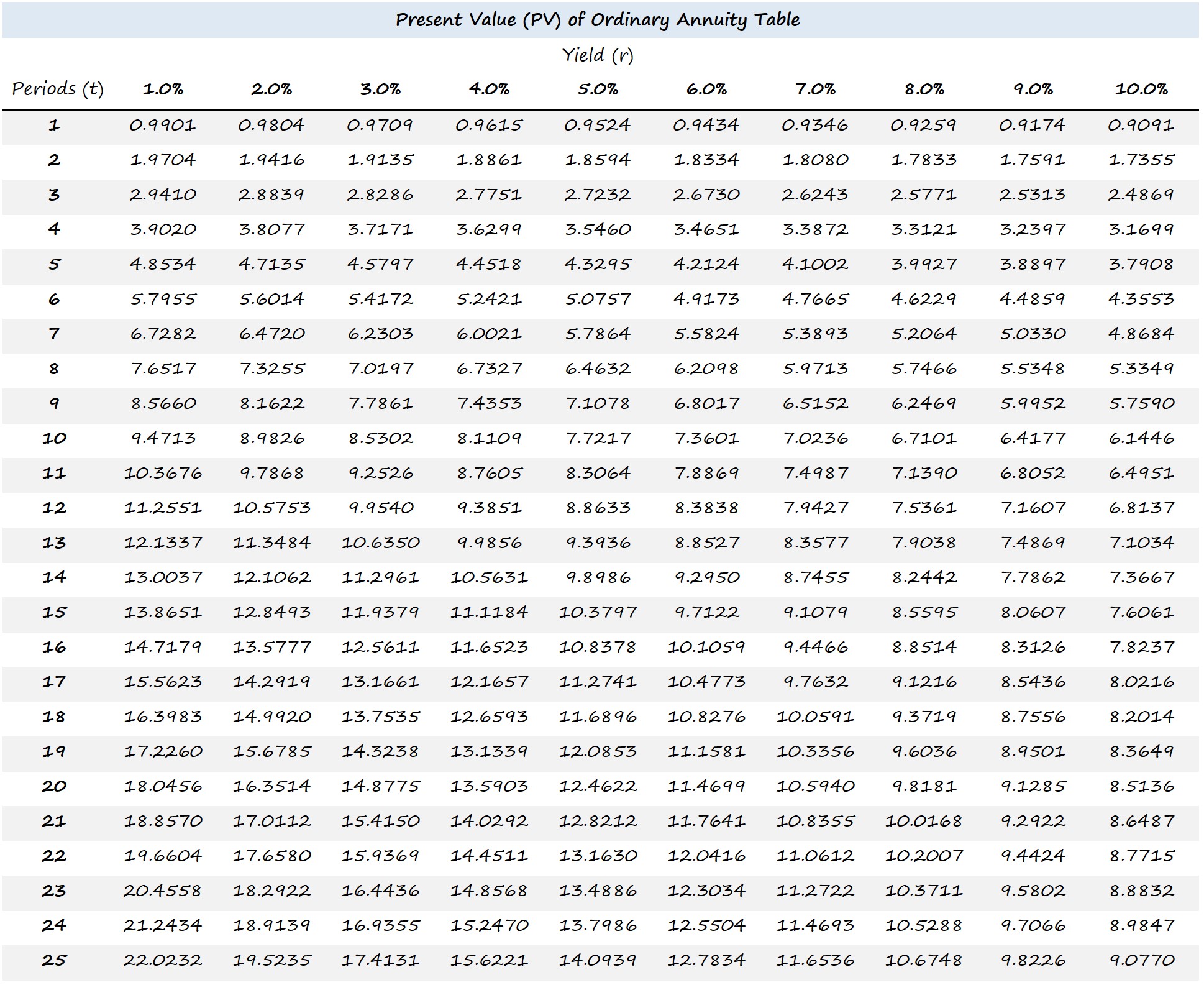
Valor presente de una tabla de vencimiento de anualidades (PV)
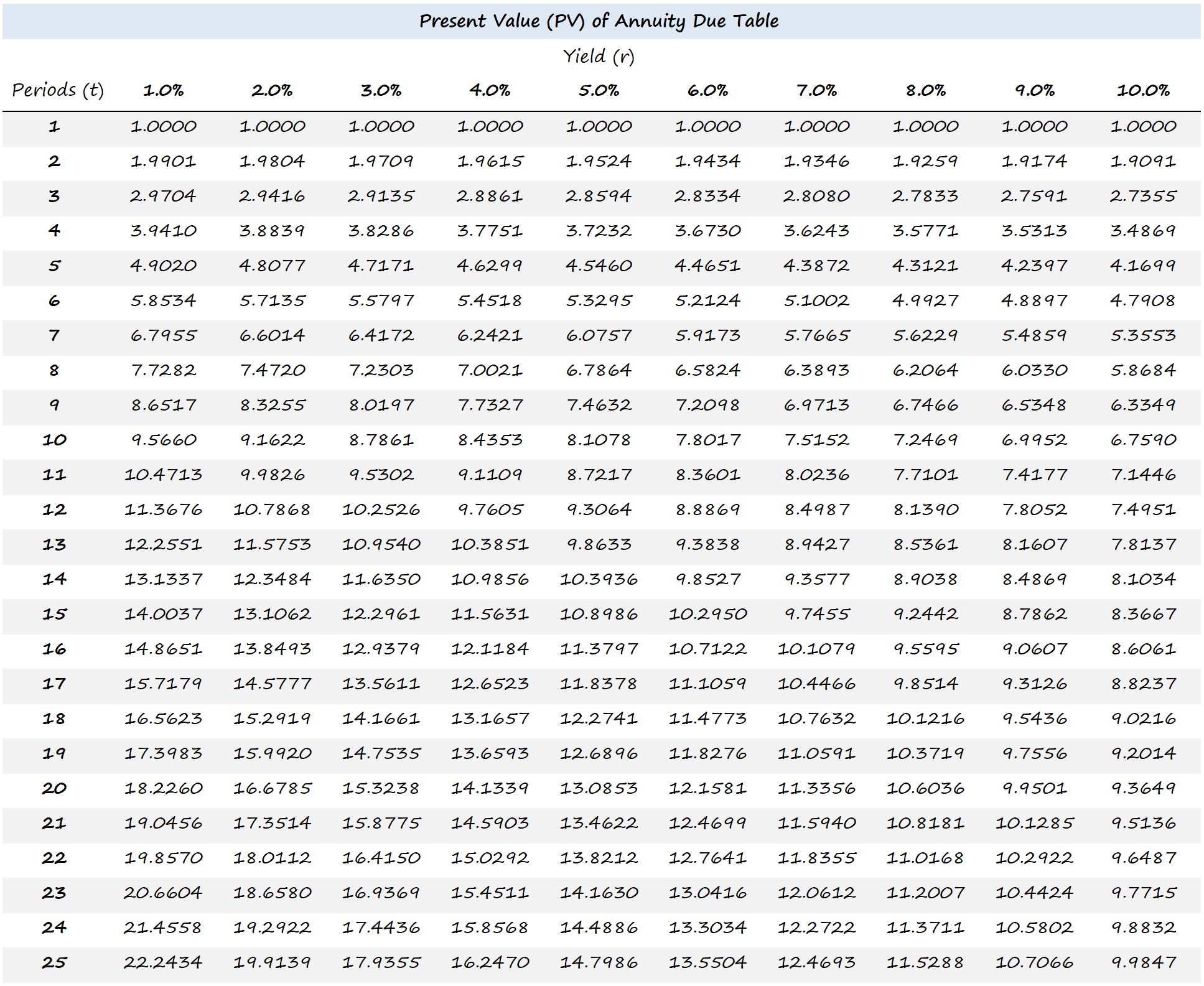
Calculadora de pensiones
Pasamos ahora a un ejercicio de modelado, al que puede acceder rellenando el siguiente formulario.
1. Supuestos sobre el bono de pensión
En nuestro ejemplo ilustrativo, calculamos el valor presente (PV) de una pensión en dos escenarios diferentes.
- Pensión ordinaria
- Pensión adeudada
Los supuestos que se enumeran a continuación deben utilizarse durante todo el ejercicio.
- Pago de anualidad = $1,000
- Retorno (r) = 5,0%
- Periodos
2. Ejemplo de cálculo del valor actual de la pensión (PV)
Primero, calculamos el valor presente (PV) de la anualidad teniendo en cuenta los supuestos relacionados con el bono.
Aquí la función de Excel «PV» se puede utilizar como se muestra a continuación.
- Valor presente (PV) = PV (r, períodos, – pago de pensión, 0, “0” o “1”)
- Valor presente (PV) = PV (5%, 20, – $1000, 0, IF (celda de tipo de anualidad = «ordinaria», 0,1))
Nota: Dado que tenemos dos escenarios, creemos un interruptor para cambiar entre las dos opciones, es decir, «IF(Annuity Type Cell =»Ordinary», 0,1)».
Los dos valores presentes (PV) calculados para el bono de anualidad son los siguientes:
- Pensión normal = $12,462
- Pensión adeudada = $13,085
3. Ejemplo de cálculo del valor de la pensión futura (FV)
A partir de ahí también podemos calcular el valor futuro (FV) usando la siguiente fórmula:
- Valor Futuro (FV) = – FV (r, t, pago de pensión, 0, “0” o “1”)
- Valor futuro (FV) = – FV (5%, 20, $1000, 0, IF (E5 = “Ordinario”, 0, 1))
Los dos montos de valor futuro (FV) calculados para el bono son los siguientes:
- Pensión normal = $33,066
- Pensión adeudada = $34,719
En el paso final, calculamos el rendimiento al vencimiento (YTM) utilizando la función “RATE” de Excel.
- Rendimiento al vencimiento (YTM) = Tasa de interés (t, pago de anualidad, 0, – FV, “0” o “1”)
- Rendimiento al vencimiento (YTM) = TASA (20, $1,000, 0, – FV, IF (E5 = “Ordinario”, 0, 1))”
En resumen, el bono tiene un rendimiento del 5,0% en ambos escenarios.
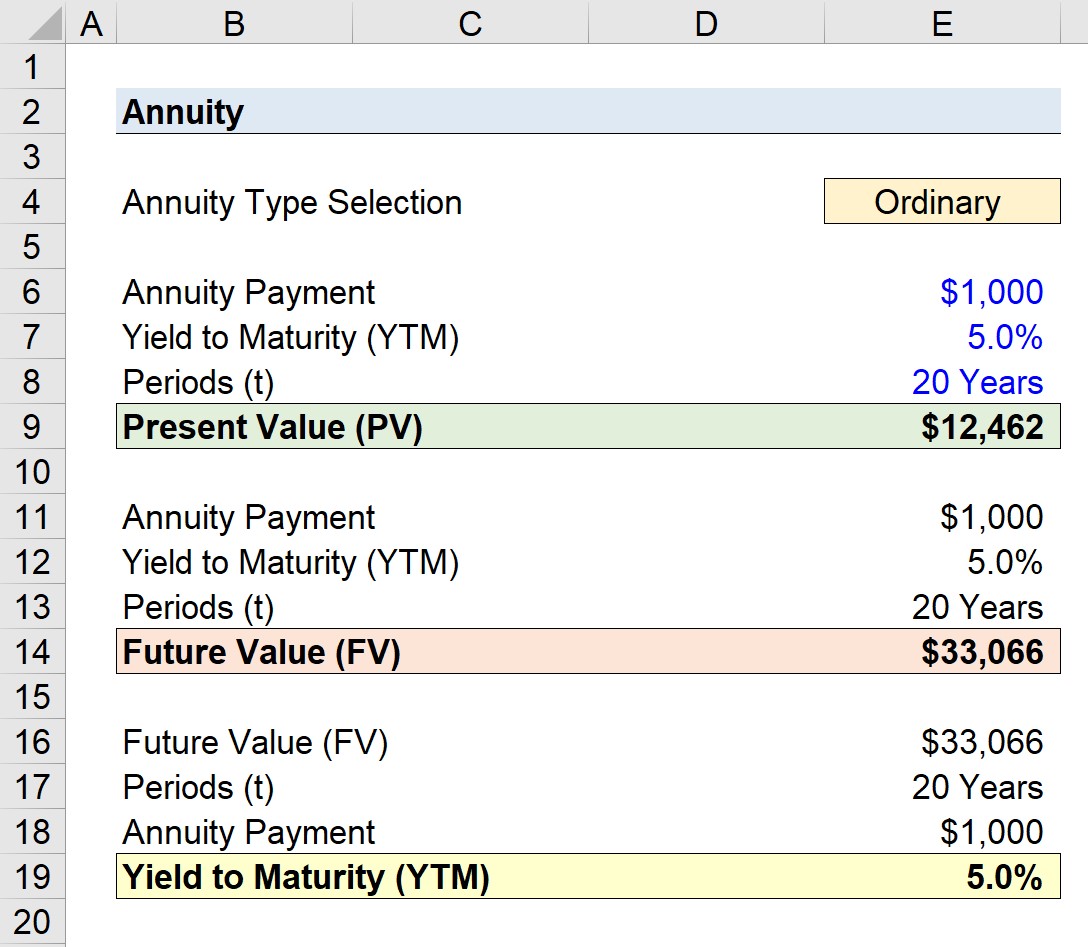
Pensión ordinaria
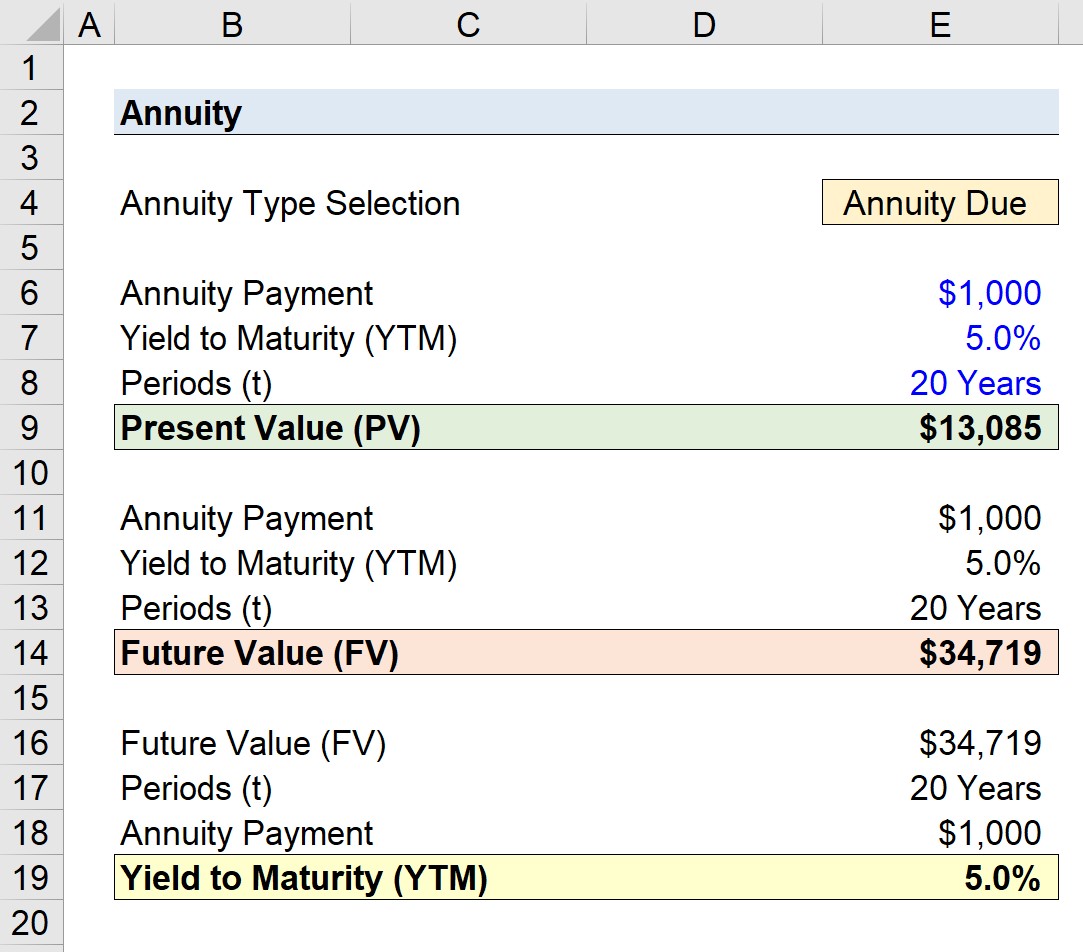
Pensión adeudada
Fórmula del Valor Actual (PV) + Calculadora
El Valor Actual (PV) es un concepto financiero fundamental que se utiliza para determinar el valor de un flujo de efectivo futuro descontado a una tasa de interés específica. Calcular el Valor Actual es crucial en la toma de decisiones de inversión y financiamiento. A continuación, te explicamos la fórmula del Valor Actual y cómo puedes utilizar una calculadora para realizar estos cálculos de manera rápida y precisa.
Fórmula del Valor Actual (PV)
La fórmula del Valor Actual se expresa de la siguiente manera:
PV = CF / (1 + r)^n
Donde:
PV = Valor Actual
CF = Flujo de efectivo futuro
r = Tasa de descuento
n = Número de periodos
La fórmula del Valor Actual nos permite determinar cuánto vale un monto futuro en términos de valor presente, considerando la tasa de interés que se aplica y el tiempo restante hasta que se reciba dicho monto.
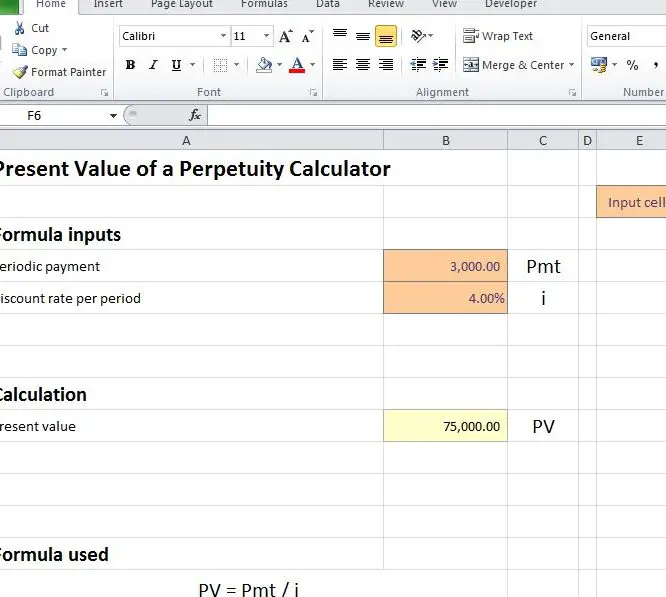
Calculadora del Valor Actual
Para facilitar el cálculo del Valor Actual, puedes utilizar una calculadora financiera o una calculadora en línea que te permita ingresar los valores del flujo de efectivo futuro, la tasa de descuento y el número de periodos. A través de esta herramienta, obtendrás el Valor Actual de manera automática y precisa.
Preguntas Frecuentes (FAQs)
¿Por qué es importante calcular el Valor Actual?
Calcular el Valor Actual es fundamental para evaluar la viabilidad de proyectos de inversión, decisiones de financiamiento y cualquier otra situación que implique flujos de efectivo futuros. Al determinar el valor presente de estos flujos, podemos tomar decisiones financieras informadas.
¿Cómo influye la tasa de descuento en el cálculo del Valor Actual?
La tasa de descuento utilizada en la fórmula del Valor Actual representa el costo de oportunidad de invertir en un proyecto en lugar de invertir en otra alternativa. A mayor tasa de descuento, menor será el Valor Actual de los flujos de efectivo futuros.
¿Qué consideraciones adicionales se deben tener en cuenta al calcular el Valor Actual?
Además de la tasa de descuento, es importante considerar la consistencia de los flujos de efectivo, la calidad de la información utilizada y la sensibilidad de los resultados a cambios en los supuestos. Estos aspectos pueden afectar la precisión de los cálculos del Valor Actual.
Esperamos que esta información te haya sido útil para comprender la fórmula del Valor Actual y cómo puedes utilizar una calculadora para realizar estos cálculos de manera efectiva. Recuerda la importancia de considerar el Valor Actual en tus decisiones financieras para maximizar el valor de tus inversiones.
[automatic_youtube_gallery type=»search» search=»Fórmula del valor actual (PV) + Calculadora» limit=»1″]
¡Buena onda! Esta fórmula del valor actual y la calculadora son sin duda un salvavidas en el mundo de las inversiones. Ya me han sacado de apuros más de una vez con mis cálculos. ¡Gracias por compartir este artículo tan útil, de verdad que me ha servido un montón! – Codebruchp
Qué buen artículo, gracias por compartir esta información tan útil. Me ha ayudado a entender mejor cómo calcular el valor actual de una inversión. ¡Muy práctico!
¡Vaya! Esta calculadora es una herramienta super útil. Me ahorrará un montón de tiempo calculando el valor actual de mis inversiones. ¡Gracias por compartirla!
Comment Author Name:
DMFAy
¡Totalmente de acuerdo! Esta fórmula y calculadora son geniales. Me han salvado en más de una ocasión cuando he tenido que hacer cálculos de inversión. ¡Gracias por el artículo!